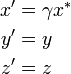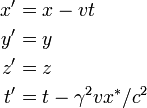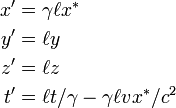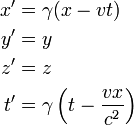Challenge to the mathematical validity of the Voigt transformation equations and hence the Theory of Relativity.
[ introduction ]
copyright december 2008 by Steve Waterman all rights reserved
A well known problem re-worded...where is the missing ten bucks ?

Three inventors go to apply for their patents at the patent office.

The clerk charged them a hundred dollars each. Later, realizing that he overcharged them; since they had filed simultaneously, the actual cost should have been only two hundred and fifty dollars.
He decided to take an early tip and pocketed a quick twenty, giving each inventor only ten dollars back.
Therefore, each has paid ninety and three times ninety is two seventy. The clerk has pocketed twenty. Two seventy and twenty is two ninety - so where is the missing ten dollars?
Regardless, of what truth the responder may speak, they hear back...
"True, you are right" and the clerk just keeps repeating...
"Therefore, each has paid ninety and three times ninety is two seventy. The clerk has pocketed twenty. Two seventy and twenty is two ninety - so where is the missing ten dollars?",
as if you should hand him the ten bucks.
The solution is to find the flaw in his statements...not in the stating of truths.
The deception is in the phrase "plus the twenty which the clerk tipped himself".
This twenty bucks should not be added to the two seventy; it should be subtracted from the two seventy.
The twenty the clerk got is part of the two seventy the three inventors spent collectively.
If you subtract the twenty from the two seventy you get the two fifty that the patent office received..
This exact same trick is employed in the Galilean equation x' = x - vt...
when the correct answer is x' = x + vt. Actually...the Galilean transformation does the opposite by subtracting when he should be adding.
|
| some working definitions
As with more things, it is always good to define things that upon occasion may seem evem simple or too obvious. This applies here and since the challenge is to the Galilean Coordinate Transformation Equations. It is logical to start with what an abscissa and a coordinate is and what a coordinate transformation is.
|
|
absciccsa
You can look at a 2D Coordinate system as a system in which a point can be defined using two values. We do this by using two perpendicular and directed lines called the abscissa(x axis) and the ordinate(y axis). The point of intersection of these two lines is called the origin denoted O(0,0). Any point can be determined as P(x,y), where x is the value in the x-axis and y is the value in the y-axis.
|
abscissal values 3 2 0 1.5
from Wikipedia...."coordinate transformation"
|
In Mathematics, the Cartesian coordinate system (also called rectangular coordinate system) is used to determine each point uniquely in a plane through two numbers, usually called the x-coordinate or abscissa and the y-coordinate or ordinate of the point. To define the coordinates, two perpendicular directed lines (the x-axis, and the y-axis), are specified, as well as the unit length, which is marked off on the two axes (see figure above). Cartesian coordinate systems are also used in space (where three coordinates are used) and in higher dimensions. |
|
A coordinate transformation is a conversion from one system to another, to describe the same space.
* such that the new coordinates of the image of each point are the same as the old coordinates of the original point.
For example, in 1D, if the mapping is a translation of 7 to the right, the coordinate of each point becomes 7 less.
* such that the old coordinates of the image of each point are the same as the new coordinates of the original point.
For example, in 1D, if the mapping is a translation of 7 to the left, the coordinate of each point becomes 7 more.
|
Way back in 1887, before the THEORY of Relativty was submitted in 1905, a set of transformation equations were also submitted...called the Voigt transformations equations.
In modern notation Voigt's transformation was
Now to attempt to expose that missing ten dollars....
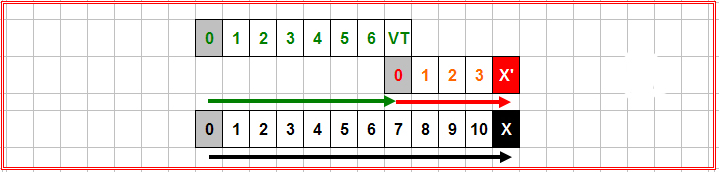
A very simple example...two frames are coincidental and have a point at 11,0.
One frame moves to the right a distance of 7, while the other does not move. It is the comparison of these two frames AFTER the Voigt transformation that is questioned. |
|








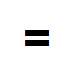
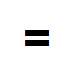
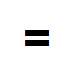
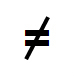

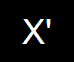



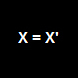
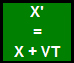












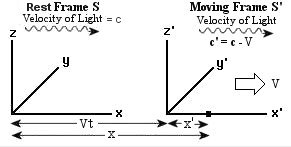
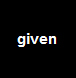

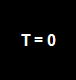


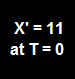



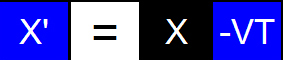



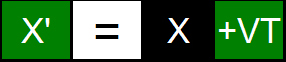












 a coordinate length of
a coordinate length of 

 nor
nor 








 is merely
is merely